Difference between revisions of "Resum astrofísica"
(Partial save) |
(Partial save) |
||
| Line 185: | Line 185: | ||
[[File:Orpols-eos.png|thumb]] | [[File:Orpols-eos.png|thumb]] | ||
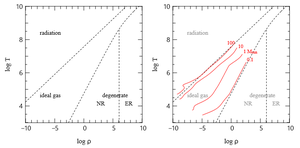
Segons $T$ i $\rho$ la presió dominant és d'una font o una altra (radiació, gas ideal, degenerat no relativista o degenerat relativista). | Segons $T$ i $\rho$ la presió dominant és d'una font o una altra (radiació, gas ideal, degenerat no relativista o degenerat relativista). | ||
==== Models politròpics estel·lars ==== | |||
$$P = K \rho^\gamma.$$ | |||
Índex politròpic: $n = \frac{1}{\gamma - 1}$. | |||
Equació de Lane-Embden: | |||
$$\frac{1}{z^2} \frac{d}{dz} \left( z^2 \frac{dw}{dz} \right) + w^n = 0,$$ | |||
$\rho = \rho_c w^n$, $r = \alpha z$, $\alpha = \left( \frac{n + 1}{4 \pi G} K \rho_c^{1/(n - 1)} \right)^{1/2}$. | |||
=== Equilibri tèrmic === | |||
Processos per transportar energia: | |||
* Difusió: moviment brownià. Conducció del calor (partícules) i difusió radiativa (fotons). | |||
* Convecció: bombolles de gas. Transporta energia de dins cap a fora i també barreja. | |||
Per temps d'escala curts: $\delta u = \delta q + \frac{P}{\rho^2}{\delta \rho}$. Això porta a la tercera equació per l'estructura estel·lar: | |||
$$\frac{\partial L_\text{loc}}{\partial m} = \varepsilon_{nuc} - \varepsilon_\nu \, \underbrace{- \frac{\partial u}{\partial t} + \frac{P}{\rho^2} \frac{\partial \rho}{\partial t}}_{\varepsilon_{gr}}.$$ | |||
Tenim $\varepsilon_{gr} = - T \frac{\partial s}{\partial t}$. A més: | |||
* $\varepsilon_{gr} > 0$: contracció, | |||
* $\varepsilon_{gr} < 0$: expansió. | |||
A la superfície, $L_{loc} = L_*$, i al centre $L_{loc} = 0$. | |||
Estat estacionari: $\varepsilon_{gr} = 0$ (derivades temporals nul·les), i $L_* = L_{nuc} - L_\nu$. | |||
==== Transport d'energia per difusió ==== | |||
Per fotons, obtenim la quarta equació d'estructura estel·lar (eq. radiatiu, vàlida per eq. td. local, i.e. $l \ll R$): | |||
$$\frac{\partial T}{\partial m} = - \frac{3}{64 \pi^2 ac} \frac{k L_{loc}}{r^4 T^3}.$$ | |||
$$\vec{F}_\text{rad} = - K_{rad} \nabla T = \frac{4}{3} \frac{ac T^3}{k \rho} \nabla T.$$ | |||
$$\nabla_{rad} := \left( \frac{\log T}{\log P} \right)_{rad} = \frac{3}{16 \pi ac G}\frac{k L_{loc} P}{m T^4}.$$ | |||
Si l'energia és únicament transportada per radiació, $\nabla_{rad}$ ens descriu la variació logarítmica de la temperatura en funció de la profunditat (expressada en termes de la pressió). | |||
==== Opacitat de Rosseland ==== | |||
$k \equiv k(\nu)$ en general. | |||
==== Transport per conducció ==== | |||
En estels degenerats els electrons han de "viatjar" més per trobar un nivell desexcitat: $l_e \gg l_{ph}$, i domina conducció. | |||
$$\vec{F}_{cond} = - K_{cond} \nabla T.$$ | |||
==== Opacitat ==== | |||
Contribucions: | |||
* Dispersió electrònica. Font important per T altes. | |||
* Absorció lliure-lliure. Electró lliure al costat d'un ió que absorbeix fotó. | |||
* Absorció lligat-lliure. Àtom s'ionitza. Depèn linealment amb la metalicitat Z. | |||
** Exemple: H<sup>-</sup>. | |||
* Absorció lligat-lligat. Excitació de l'àtom. | |||
* Molècules i pols: per estels freds. | |||
* Opacitat conductiva: es pot descriure com una opacitat amb coeficient $k_{cond}$. | |||
==== Règims en l'opacitat estel·lar ==== | |||
... | |||
==== Lluminositat d'Eddington ==== | |||
Conducció radiativa implica gradient de T implica gradient de P_{rad}. Per eq. tenim que $\nabla P_{rad} < \nabla P_\text{eq. hs.}$, que implica: $L_{loc} < \frac{4 \pi c G m}{k} =: L_{loc, Edd}$. A la superfície tenim: | |||
$$L_* < L_\text{Edd} := \frac{4 \pi c G M}{k},$$ | |||
on $k$ és l'opacitat a la fotoesfera de l'estel. Si l'opacitat és aprox. constant a dins de l'estel, llavors $L_{Edd}$ només depèn de $M$, i $L_{Edd} \propto M$. Estels seq. principal són tals que $L_* \propto M^x$ amb $x > 1$, per tant existirà una massa màxima. | |||
==== Transport per convecció ==== | |||
Definim '''exponent adiabàtic''': | |||
$$\gamma_{ad} \equiv \left( \frac{\partial \log P}{\partial \log \rho} \right)_{ad}$$ | |||
Si $\gamma_{ad} = cte. \implies P \propto \rho^{\gamma_{ad}}$. | |||
'''Gradient adiabàtic de temperatura''': | |||
$$\nabla_{ad} \equiv \left( \frac{\partial \log T}{\partial \log P} \right)_{ad}$$ | |||
Si $\nabla_{ad} = cte. \implies T \propto P^{\nabla_{ad}}$ | |||
que ens descriu el comportament de la temperatura sota una compressió o expansió adiabàtica. | |||
'''Criteri general per a l'estabilitat contra processos convectius''': | |||
$$\frac{d \log \rho}{d \log P} > \frac{1}{\gamma_{ad}}.$$ | |||
Si el transport d'energia de l'estel és essencialment radiatiu, $\nabla \approx \nabla_{rad}$. El '''criteri de Schwarzschild''' estableix llavors que '''una capsa és estable contra processos convectius''' si es dona la condició: | |||
$$\nabla_{rad} = \frac{3}{16 \pi ac G} \frac{P}{T^4} \frac{kL_{loc}}{m} < \nabla_{ad}.$$ | |||
Sitacions on hi ha convecció (no es compleix el criteri de Sch.): | |||
* Regions molt opaques (k elevat). Convecció eficient. Normalment estels de baixa massa. | |||
* Fluxe d'energia elevat. Per exemple al nucli amb reaccions termonuclears. | |||
* Valors de $\nabla_{ad}$ baixos, com regions de l'estel parcialment ionitzades o a T baixa. | |||
== Bloc 3. Processos nuclears estel·lars == | |||
Latest revision as of 22:02, 27 June 2022
Bloc 1. Formació estel·lar
El medi interestel·lar
Conceptes
- ISM: Interstellar medium - medi interestel·lar
- Hi ha pols, gas, ions/àtoms/molècules o electrons lliures que imposen condicions a la transferència radiativa/termodinàmica del medi.
- IGM: Intergalactic medium - medi intergalàctic
- ICM: Intracluster medium
- Hi ha filaments causats per l'energia fosca.
- Estels neixen de gas i pols. Tenen un cicle de vida (material es torna a l'ISM).
- Primera població d'estrelles: població III (baixa metal·licitat, molt massives).
- Límit d'homogeneïtat de l'univers: 50-150 megapàrsecs.
Components del medi interestel·lar
- Hidrogen: 70% (H I, H II, H2).
- Heli: 28%
- 2% restant: carboni, silici, ...
Major part de l'H difós a l'ISM: núvols d'hidrogen neutre H I. No produeix línies d'emissió, però es podria detectar a través de línies d'absorció UV si dona la casualitat que les atravesa.
Per detectar H neutre: emissió ràdio quan es canvia l'espí de l'electró r/ el protó (antialineament <-> alineament). $\lambda = 21.1 \text{ cm}$. Es dona moooolt infreqüentment (temps de vida de milions d'anys). Estimulat per xocs (temps de vida de centenars d'anys).
Pols interestel·lar
Extenció estel·lar: causada per la pols. Efecte de la dispersió (scattering) i l'absorció dels fotons emesos per estels.
$$m_\lambda = M_\lambda + 5 \log_{10} \left( \frac{d}{10 \text{ pc}} \right) + A_\lambda.$$
$m_\lambda - m_{\lambda,0} = - 2.5 \log_{10}\left( \frac{I_\lambda}{I_{\lambda, 0}} \right)$, on el subíndex 0 vol dir que no considerem l'extinció, i $I_\lambda = I_{\lambda, 0} e^{- \tau_\lambda}$, on $\tau_\lambda$ és l'espessor òptic. Per tant $A_\lambda = 1.086 \tau_\lambda$.
Assumint homogeneitat en la columna d'un núvol de pols: $\tau_\lambda = \sigma_\lambda N_d$, on $N_d$ és la columna de densitat de pols i $\sigma_\tau$ la secció eficaç (per ex: Gustav Mie va prendre $\sigma_g = \pi a^2$, la secc. transversal d'un àtom esfèric).
Coeficient d'extinció: [math]\displaystyle{ Q_\lambda := \sigma_\lambda / \sigma_g }[/math].
Límits fenomenològics (Mie): $$\sigma_\lambda = \begin{cases} a^3/\lambda & (\lambda \gtrsim a), \\ a^2 & (\lambda \ll a) \end{cases}$$
$A_\lambda$ depèn de $\lambda \implies$ longituds d'ona llargues (vermell) es dispersaran més que les curtes (blau). Per tant els objectes es veuran més vermells a través d'un núvol. Per contra, si observem en la direcció en què es dispersa més el blau, veurem més blau (nebulosa de reflexió).
Aproximacions de Mie funcionen bé per longituds d'ona relativament grans. Realitat: per energies més altes hi ha desviacions: grafits, hidrocarburs policíclics (molècules complexes orgàniques), silicats.
Núvols moleculars
Núvols de pols poden protegir hidrogen de la radiació UV. Es forma $H_2$, que es detecta mitjançant traçadors.
- Núvols moleculars difosos: d'hidrogen atòmic. $A_V \in (1, 5)$. $n \sim 10^9 \text{m}^{-3}, M \sim 3-100 M_\odot$.
- Núvols moleculars gegants: enormes ($l \gtrsim 50 \text{ pc}$) de pols i gas. $n \sim 10^8 \text{ m}^{-3}, M \sim 10^5 - 10^6 M_\odot$.
- Glòbuls de Bok: geometries esfèriques. $A_V \gtrsim 10$. $n \gtrsim 10^{10} \text{ m}^{-3}, M \sim 1-1000 M_\odot$.
Distribució del gas a l'ISM
- Gas "coronal": molt calent (rep radiació de tot el disc), poc dens, omple l'halo galàctic. Traçat bé: línies d'emissió. Escalfat/ionitzat per xocs de SN, vent disc galàctic, o associacions OB.
- Gas calent ionitzat: moderadament calent (8000 K), poc dens. Font d'ionització incerta. Traçat: línies d'absorció, emissió línia H alfa.
- Gas atòmic neutre: fred (100 K), composat de núvols d'hidrogen (cold neutral medium). Entre núvol i núvol, hi ha gas calent ionitzat. Traçat: línia 21 cm o línies absorció.
- Gas molecular: fred, concentrat en els núvols moleculars. Regió de formació estelar. Traçat mitjançant línies d'emissió.
- Raigs còsmics (CRs): partícules carregades accelerades en explosions de supernova, en xocs forts dels vents estel·lars d'estels joves, o perduts fora de la Glàxia en nuclis de galàxies actius, etc.
- Ampli rang d'energies.
- 50% protons, 25% partícules alfa, 13% nuclis C, N, O, <1% electrons/positrons, <0.1% fotons.
- Acumulen 1/3 de la densitat total d'energia no-tèrmica de l'univers. Ionitzen àtoms/molècules. Això fa que augmenti la temperatura de l'ISM.
- Altres fonts de calentament: ionització del Carboni amb fotons UV/X, o absorció de fotons.
- Balanç termodinàmic: emetent fotons en infraroig ($\lambda_\text{IR} \gtrsim r_\text{pols}$ permet alliberar aquest excés d'energia sense que es reabsorbeixi).
Formació de protoestels
- Núvols moleculars de l'ISM --> protoestels --> estels (quan comencen a cremar).
- Formació degut al col·lapse d'un núvol molecular.
- Teorema del virial:
- $2K = -U (= |U|)$: equilibri estable.
- $2K > |U|$: núvol s'expandeix.
- $2K < |U|$: núvol col·lapsa.
Criteri de Jeans
Considerem núvol molecular amb densitat constant $\rho_0$. Negligim rotació gas, camps magnètics o turbolències hidrodinàmiques dins del núvol. Si definim $N = M_c/(mu m_H)$, amb $\mu$ pes molecular mig, la massa mínima perquè col·lapsi és: $$M_J \approx \left( \frac{5 K_B T}{G \mu m_H} \right)^{3/2} \left( \frac{3}{4 \pi \rho_0} \right)^{1/2}.$$
I el radi mínim és: $$R_J \approx \left( \frac{15 K_B T}{4 \pi G \mu m_H \rho_0} \right)^{1/2}.$$
Si el nucli de gas està dins d'un GMC, llavors hi ha pressió exterior. Correcció: prenem com a límit la massa de Bonnor-Ebert: $$M_\text{BE} = \frac{c_\text{BE} v_T^4}{P_0^{1/2} G^{3/2}},$$ $v_T := \sqrt{K_B T/(\mu m_H)}$.
Col·lapse gravitacional del núvol molecular
- Més simplificacions:
- Durant el col·lapse, els gradents de pressió són molt petits (no els considerem). Això implica un col·lapse en caiguda lliure.
- Col·lapse isotèrmic: l'energia pot. grav. alliberada no es torna a absorbir.
Fem una EDO considerant les forces que actuen sobre $dm(r, t)$, i arribem a que la pressió es desprecia a l'EDO, i que el temps de caiguda lliure és: $$t_{ff} = \left( \frac{3 \pi}{32} \frac{1}{G \rho_0} \right)^{1/2}.$$
Fragmentació dels núvols moleculars
Masses dels núvols moleculars massa altes (no veiem estels d'aquestes masses). Hi ha fragmentació. Això és degut al fet $M_J \propto n^{-1/2}$. Mentre el núvol col·lapsa el criteri es compleix per masses més petites, que fa que es fragmenti.
- Quan el núvol col·lapsa, cada cop és més opac i deixa de complir-se la condició isoterma. En cert moment es restaura l'eq. hidrostàtic: diem que ha nascut el protoestel.
- Gas circumandant continua caient sobre el protoestel (acreció). Part de l'energia gravitacional escalfa el protestel, part es radia al medi circumdant.
- Evolució protoestels:
- Classe 0: acreció esfèrica.
- Classe 1: formació de jets bipolars. Disc d'acreció gruixut.
- Classe 2: fase "estel T Tauri". Disc d'acreció gruixut.
- Classe 3: disc d'acreció prim, formació de planetes.
Bloc 2. Estructura estel·lar
Equilibri hidrostàtic
Condicions d'eq. hs: $$\frac{\partial r}{\partial m} = \frac{1}{4 \pi r^2 \rho}, \frac{dP}{dm} = - \frac{Gm}{4 \pi r^4}$$ Juntament amb l'equació d'estat de l'estel (si és $P = P(\rho)$, i.e. no depèn de T, s'anomena politròpica, llavors estructura mecànica i tèrmiques desacoblades).
Temps dinàmic
$t_\text{din}$: ens indica quan de ràpid canvia l'estel quan es pertorba respecte l'eq.
- La podem trobar dimensionalment:
$$t_\text{ff, estel} \approx \sqrt{\frac{R^3}{GM}} \approx t_\text{ff, núvol}.$$
- O suposant que la gravetat desapareix sobtadament, el temps que es requereix perquè l'estel explotés (una ona de so atrevessés l'estel):
$$t_{exp} \approx \frac{R}{\bar{c}_s},$$ on $\bar{c}_s$ és la velocitat mitja del so a l'estel.
Cas del sol: $t_{\text{din}, \odot} \approx 1600 \text{ s} \ll t_{\text{age}, \odot} \approx 4.6 \text{ Gyr}$.
- Qualsevol desviació de l'eq. dona lloc a canvis ràpids que el porten ràpidament a l'eq. Si no s'arriba a eq. de nou, porta directament a col·lapse o explosió.
- Hi ha petites oscil·lacions vora l'eq. amb durada $t_\text{din}$.
- $t_\text{din}$ és molt més petit que el temps de canvi de l'estrella, així que té evolució quasi-estàtica.
Teorema del Virial
Es desenvolupa començant per la 2a condició d'eq. i multiplicant-la pel volum $V = (4/3) \pi r^3$ i $dm$, i integrant de $0$ a $M$. RHS és l'en. pot. grav., i la de l'esquerra s'integra per parts (les condicions de vora de la pressió són nul·les). Usem eq. gas ideal i que la en. cinètica per partícula és $\varepsilon_k = (3/2) K_B T$. Arribem a: $$E_\text{int} = - \frac{1}{2} E_\text{grav}.$$
Donada eq. d'estat genèrica $u = \phi P/\rho$: $$E_\text{int} = - \frac{1}{3} \phi E_\text{grav}.$$
Estima de la temperatura mitja d'un estel
...
Estima de l'energia total d'un estel
$$E_\text{tot} = E_\text{grav} + E_\text{int} + E_\text{kin}.$$
L'estel està lligat si $E_\text{tot} < 0$. Eq. hidrostàtic implica $E_\text{kin} = 0$. $$E_\text{tot} = \frac{\phi - 3}{\phi} E_\text{int}.$$
Els estels radien. Per mantindre l'eq., part de la radiació s'absorbeix (i l'estel s'escalfa!) i altra es perd.
Si un estel està dominat per pressió de radiació, $E_\text{int} = - E_\text{grav} \implies E_\text{tot} = 0$. Una pertorbació el fa inestable.
Temps d'escala estelars
- Temps dinàmic: escala del temps que triga un estel en reaccionar a pertorbacions r/ eq. hs: $t_\text{din} \approx \sqrt{\frac{R^3}{GM}}$.
- Temps tèrmic/de Kelvin-Helmholtz: canvis tèrmics $t_\text{KH} = \frac{E_\text{int}}{L} \approx \frac{GM^2}{2 RL}$.
- Temps nuclear: temps durant el qual l'estel manté reaccions nuclears al seu interior.
- $t_{nuc} \gg t_{KH} \gg t_{din}$.
Equacions d'estat
- Estels no estan en eq. td. global però sí local en diferents regions.
- Recorregut lliure mig: $l_\text{ph} = (k \rho)^{-1}$, on $k$ és el coef. d'opacitat (secció eficaç). Diferència de temperatures molt petita per aquesta distància, ens permet definir eq. td. local (LTE). Per tant T ben definida a l'estel.
Gas de partícules lliures
$$n = \int_0^\infty n(p) dp$$ $$U = \int_0^\infty \varepsilon_p n(p) dp = n \langle \varepsilon_p \rangle$$ $$P = \frac{1}{3} \int_0^\infty p v_p n(p) dp = \frac{1}{3} n \langle p v_p \rangle$$
- No relativista: $P = \frac{2}{3} U$,
- (Ultra)relativista: $P = \frac{1}{3} U$.
Gas ideal
Típic.
Pressió de radiació
$$P = \frac{1}{3} a T^4.$$
Pressió mixta de gas i radiació
$$P = \frac{1}{3} a T^4 + \frac{R}{\mu} \rho T.$$
Gas degenerat
Fermions: cada estat només pot tenir una partícula. La distribució de moments té un $n_\text{max}(p)$ (M-B (clàssic) vs. règim quàntic).
Per tant $\exists p_\text{max} = p_\text{F}, \varepsilon_F$.
La pressió de degeneració d'un gas d'electrons és: $$P = \frac{(3 \pi^2)^{2/3}}{5} \frac{\hbar^2}{m_e} \left[ \left( \frac{Z}{A} \right) \frac{\rho}{m_H} \right]^{{5}/{3}}.$$
El límit de Chandrasekhar
Pressió de degeneració pot contindre el col·lapse gravitatori de les nanes blanques. Chandrasekhar va donar una massa màxima per les nanes blanques. Pressió de degeneració ultrarrelativista: $$P = \frac{(3 \pi^2)^{1/3}}{4} \hbar c \left[ \left( \frac{Z}{A} \right) \frac{\rho}{m_H} \right]^{{4}/{3}}.$$
$$M_\text{Ch} \approx \frac{3 \sqrt{2 \pi}}{8} \left( \frac{\hbar c}{G} \right)^{3/2} \left[ \left( \frac{Z}{A} \right) \frac{1}{m_H} \right]^2$$
Per $Z/A = 0.5$, $M_\text{Ch} = 1.44 M_\odot$ (massa límit de Chandrasekhar).
Règims de l'eq. d'estat estel·lar
Segons $T$ i $\rho$ la presió dominant és d'una font o una altra (radiació, gas ideal, degenerat no relativista o degenerat relativista).
Models politròpics estel·lars
$$P = K \rho^\gamma.$$
Índex politròpic: $n = \frac{1}{\gamma - 1}$.
Equació de Lane-Embden: $$\frac{1}{z^2} \frac{d}{dz} \left( z^2 \frac{dw}{dz} \right) + w^n = 0,$$ $\rho = \rho_c w^n$, $r = \alpha z$, $\alpha = \left( \frac{n + 1}{4 \pi G} K \rho_c^{1/(n - 1)} \right)^{1/2}$.
Equilibri tèrmic
Processos per transportar energia:
- Difusió: moviment brownià. Conducció del calor (partícules) i difusió radiativa (fotons).
- Convecció: bombolles de gas. Transporta energia de dins cap a fora i també barreja.
Per temps d'escala curts: $\delta u = \delta q + \frac{P}{\rho^2}{\delta \rho}$. Això porta a la tercera equació per l'estructura estel·lar: $$\frac{\partial L_\text{loc}}{\partial m} = \varepsilon_{nuc} - \varepsilon_\nu \, \underbrace{- \frac{\partial u}{\partial t} + \frac{P}{\rho^2} \frac{\partial \rho}{\partial t}}_{\varepsilon_{gr}}.$$ Tenim $\varepsilon_{gr} = - T \frac{\partial s}{\partial t}$. A més:
- $\varepsilon_{gr} > 0$: contracció,
- $\varepsilon_{gr} < 0$: expansió.
A la superfície, $L_{loc} = L_*$, i al centre $L_{loc} = 0$.
Estat estacionari: $\varepsilon_{gr} = 0$ (derivades temporals nul·les), i $L_* = L_{nuc} - L_\nu$.
Transport d'energia per difusió
Per fotons, obtenim la quarta equació d'estructura estel·lar (eq. radiatiu, vàlida per eq. td. local, i.e. $l \ll R$): $$\frac{\partial T}{\partial m} = - \frac{3}{64 \pi^2 ac} \frac{k L_{loc}}{r^4 T^3}.$$
$$\vec{F}_\text{rad} = - K_{rad} \nabla T = \frac{4}{3} \frac{ac T^3}{k \rho} \nabla T.$$
$$\nabla_{rad} := \left( \frac{\log T}{\log P} \right)_{rad} = \frac{3}{16 \pi ac G}\frac{k L_{loc} P}{m T^4}.$$ Si l'energia és únicament transportada per radiació, $\nabla_{rad}$ ens descriu la variació logarítmica de la temperatura en funció de la profunditat (expressada en termes de la pressió).
Opacitat de Rosseland
$k \equiv k(\nu)$ en general.
Transport per conducció
En estels degenerats els electrons han de "viatjar" més per trobar un nivell desexcitat: $l_e \gg l_{ph}$, i domina conducció. $$\vec{F}_{cond} = - K_{cond} \nabla T.$$
Opacitat
Contribucions:
- Dispersió electrònica. Font important per T altes.
- Absorció lliure-lliure. Electró lliure al costat d'un ió que absorbeix fotó.
- Absorció lligat-lliure. Àtom s'ionitza. Depèn linealment amb la metalicitat Z.
- Exemple: H-.
- Absorció lligat-lligat. Excitació de l'àtom.
- Molècules i pols: per estels freds.
- Opacitat conductiva: es pot descriure com una opacitat amb coeficient $k_{cond}$.
Règims en l'opacitat estel·lar
...
Lluminositat d'Eddington
Conducció radiativa implica gradient de T implica gradient de P_{rad}. Per eq. tenim que $\nabla P_{rad} < \nabla P_\text{eq. hs.}$, que implica: $L_{loc} < \frac{4 \pi c G m}{k} =: L_{loc, Edd}$. A la superfície tenim: $$L_* < L_\text{Edd} := \frac{4 \pi c G M}{k},$$ on $k$ és l'opacitat a la fotoesfera de l'estel. Si l'opacitat és aprox. constant a dins de l'estel, llavors $L_{Edd}$ només depèn de $M$, i $L_{Edd} \propto M$. Estels seq. principal són tals que $L_* \propto M^x$ amb $x > 1$, per tant existirà una massa màxima.
Transport per convecció
Definim exponent adiabàtic: $$\gamma_{ad} \equiv \left( \frac{\partial \log P}{\partial \log \rho} \right)_{ad}$$ Si $\gamma_{ad} = cte. \implies P \propto \rho^{\gamma_{ad}}$.
Gradient adiabàtic de temperatura: $$\nabla_{ad} \equiv \left( \frac{\partial \log T}{\partial \log P} \right)_{ad}$$ Si $\nabla_{ad} = cte. \implies T \propto P^{\nabla_{ad}}$ que ens descriu el comportament de la temperatura sota una compressió o expansió adiabàtica.
Criteri general per a l'estabilitat contra processos convectius: $$\frac{d \log \rho}{d \log P} > \frac{1}{\gamma_{ad}}.$$
Si el transport d'energia de l'estel és essencialment radiatiu, $\nabla \approx \nabla_{rad}$. El criteri de Schwarzschild estableix llavors que una capsa és estable contra processos convectius si es dona la condició: $$\nabla_{rad} = \frac{3}{16 \pi ac G} \frac{P}{T^4} \frac{kL_{loc}}{m} < \nabla_{ad}.$$
Sitacions on hi ha convecció (no es compleix el criteri de Sch.):
- Regions molt opaques (k elevat). Convecció eficient. Normalment estels de baixa massa.
- Fluxe d'energia elevat. Per exemple al nucli amb reaccions termonuclears.
- Valors de $\nabla_{ad}$ baixos, com regions de l'estel parcialment ionitzades o a T baixa.