Estrelles: magnituds observables i propietats físiques
Introducció sobre escales
- Paral·laxi trigonomètrica: angle [math]\displaystyle{ p }[/math] (veure figura 1)
- 1 parsec = distància que tenim amb una estrella amb [math]\displaystyle{ p = 1'' }[/math] = 3.26 anys llum
- Estrelles d'una mateixa galàxia estan separades típicament per una distància de l'ordre dels parsecs
- [math]\displaystyle{ 1 \text{ any llum} \approx 9.46\cdot10^{12} \text{ km} \approx 10^{13} \text{ km} }[/math]
- [math]\displaystyle{ 1 \text{ UA} = 597 870 000 \text{ km} \approx 8.317 \text{ minuts de llum} }[/math]
|
|
Compte amb la literatura anglesa! Pels anglesos bilió és [math]\displaystyle{ 10^9 }[/math], no [math]\displaystyle{ 10^11 }[/math]. |
- Pròxima centauri: rebem la llum emesa fa aproximadament 4 anys
- Andròmeda: l'estem veient com és fa 2 milions d'any
- Unitats de massa que s'utilitzen: masses solars (per estrelles, i inclús per galàxies), masses terrestres (per planetes gasosos), masses de Júpiter (per planetes gasosos)
- Edat univers: la donem tal qual, com 14 000 milions d'anys.
- L'univers està majoritàriament buit. Densitat d'aproximadament [math]\displaystyle{ 5 \frac{\text{protons}}{\text{m}^3} }[/math]
- Densitat mitjana del Sol: semblant a la de l'aigua 1.4 g/cm^3
- Densitat de Júpiter un 20% menor a la de l'aigua (així que si tinguèssim una piscina lo suficientment gran, flotaria en aquesta)
Tema 1. Estrelles: magnituds observables i propietats físiques
- (fins fa dos anys) L'element bàsic per extreure informació del cosmos més enllà de l'atmosfera terrestre són els fotons (musons que interactuen amb la matèria). (tot i que ara hi ha les ones gravitacionals, els neutrins, etc., però tot això encara és bastant nou)
- Usarem l'àtom de Bohr: un nucli atòmic i uns orbitals quantitzats. Amb això ens és prou per conèixer les interaccions dels fotons amb la matèria.
- Excitació: d'estat fonamental a un estat superior. (tant si és excitació com desexcitació: [math]\displaystyle{ \Delta E = | E_j - E_i | = h \nu }[/math], on [math]\displaystyle{ h = 6.626 \cdot 10^{-34} \text{J} \cdot \text{s} = 6.626 \cdot 10^{-27} \text{erg} \cdot \text{s} }[/math] constant de Planck)
- Ionització: electró és lliberat de l'àtom. Generalment l'energia necessària és de l'ordre d'uns quants electronvolts (1 electron-volt = 1 eV = [math]\displaystyle{ 1.6022 \cdot 10^{-19} \text{J} }[/math])
- Reaccions nuclears de fisió o fusió és milions de vegades més energètiques que les reaccions químiques.
- Recombinació: electró lliure és capturat per un àtom i emet el fotó correponent.
- Gasos donen un espectre continu per les densitats altes (estrelles com el Sol), líquids i sòlids no perquè les densitats són més baixes.
- Les construccions atòmiques han de ser a temperatures de baixes, perquè si no quan dos àtoms s'intenten unir xoquen i "hasta luego lucas".
Espectre continu/radiació contínua
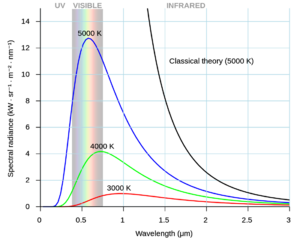
- Amb molt bona aproximació, molts objectes (com per exemple les estrelles) emeten com un cos negre. Així doncs, podem descriure molt bé la seva distribució d'energia com una distribució de Planck de cos negre.
- Cos negre: tota la energia que incideix en ell la reflecteix, així que no absorbeix cap.
- Radiació de cos negre: se suposa que és del tipus tèrmic (és la que utilitzarem; es diu així perquè té a veure amb la temperatura del cos).
@TODO: inserir effectivetemperature_extraterrestrial.png
Llei de Planck
Llei de Planck: [math]\displaystyle{ I(\nu, T) = \frac{2 h \nu^3}{c^2} \frac{1}{e^{\frac{h\nu}{K_B T}} - 1} }[/math], [math]\displaystyle{ K_B = 1.38 \cdot 10^{-23} \text{ J/K} }[/math] és la constant de Boltzman. [math]\displaystyle{ I(\nu, T) }[/math] és l'energia per unitat de temps, emesa per unitat d'àrea per radiador, observada per unitat d'angle sòlid i mesurada per unitat de freqüència.
- Hi ha més informació sobre aquesta llei al Campus Virtual.
- A vegades s'integra sobre una esfera i apareix un factor pi a la fòrmula (?)
- I és una intensitat específica perquè és sobre una freqüència específica.
[math]\displaystyle{ \Delta E = I \cos \theta \Delta A \cdot \Delta \nu \cdot \Delta \Omega \cdot \Delta t }[/math] (veure F.1)
Interludio de probabilitat random:
- [math]\displaystyle{ x, y }[/math] variables aleatòries
- [math]\displaystyle{ p(x) dx = p(y) dy }[/math]
- [math]\displaystyle{ p(y) = p(x) \left( \frac{dx}{dy} \right) }[/math]
[math]\displaystyle{ I'(\lambda, T) = I(\nu, T) \left| \frac{d\nu}{d\lambda} \right| = I(v(\lambda), T) \cdot \frac{\nu^2}{c} }[/math]
[math]\displaystyle{ I'(\lambda, T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda K_B T}}} }[/math]
Llei de Stefan-Boltzmann
Respon la pregunta: quina és la quantitat de potència emesa a un hemisferi? (integrant sobre totes les freqüències)
Flux: [math]\displaystyle{ F(T) = \int_\nu \iint_\text{hemisferi} I(\nu, T) \cdot \cos \theta d\nu d\Omega = \int_0^\infty I(\nu, T) d\nu \int_0^{2\pi} d\phi \int_0^{\frac{\pi}{2}} d\theta \cos \theta \sin \theta = }[/math] [math]\displaystyle{ = \pi \int_0^\infty d\nu I(\nu, T) = \frac{2 \pi h}{c^2} \int_0^\infty \frac{\nu^3}{e^\frac{h\nu}{K_B T} - 1} d\nu = \frac{2 \pi h}{c^2} \left( \frac{K_B T}{h} \right)^4 \int_0^\infty \frac{u^3}{e^u - 1} du = \frac{2 \pi^5 K_B^4}{15 c^2 h^3} T^4 = \sigma_\text{SB} T^4 }[/math]
[math]\displaystyle{ \sigma_\text{SB} = 5.67 \cdot 10^{-8} W m^{-2} K^{-4} }[/math] (constant d'Stefan-Boltzmann; no confondre amb la constant de Boltzmann)
- Catàstrofe ultraviolada (altes energies): bàsicament sortia una integral que divergia.
Boltzmann:
- S'aplicava la distribució (de probabilitats) de Boltzmann: [math]\displaystyle{ P(\epsilon_i) \propto e^{-\frac{\epsilon_i}{K_B T}} }[/math] (on [math]\displaystyle{ \epsilon_i }[/math] és un estat d'energia)
- [math]\displaystyle{ \lt E\gt = \frac{\int_0^\infty EP(E) dE}{\int_0^\infty P(E) dE} = K_B T }[/math]
Planck:
- [math]\displaystyle{ \epsilon_i = n h \nu \; (n = 1, 2, 3, \dots) }[/math]
- [math]\displaystyle{ \lt E\gt = \frac{\sum_{n=0}^\infty n h \nu P(n h \nu)}{\sum_{n=0}^\infty P(n h \nu)} = K_B T \left( \frac{\frac{h \nu}{K_B T}}{e^{\frac{h \nu}{K_B T}} - 1} \right) }[/math]
Llei de Wien
[math]\displaystyle{ \lambda_\text{màx} = \frac{b}{T} }[/math], on [math]\displaystyle{ b = 2.8977685 \cdot 10^{-3} \text{m} \cdot \text{K} }[/math] (constant de Wien)
Outro
- No hi ha cap objecte natural que emeti tota la seva radiació a una sola freqüència. L'energia que meten acostuma a distribuir-se en un rang ampli de freqüències. Aquesta distribució ens pot permetre obtenir informació molt valiosa sobre les propietats físiques de l'objecte.
@TODO: Include "Hydrogen Absorption Spectra" figure from "Discovering the universe. Eighth edition".
Lleis de Kirchoff
The empirical laws of spectrum analysis are commonly known as Kirchhoff's Three Laws of Spectroscopy as follows:
- A hot solid, liquid or dense gas produces a continuous spectrum.
- A hot, low-density gas produces an emission-line spectrum.
- A continuous spectrum source viewed through a cool, low-density gas produces an absorption-line spectrum.
@TODO: COPIAR TOT EL QUE HI HA AL FULL DEL DIVENDRES
Espectroscopia
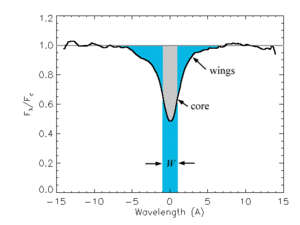
El que interessa d'una ratlla d'absorció no és la seva forma, sinó de la seva àrea.
- L'àrea es mesura amb l'amplada equivalent.
- Veure F.2.
Amplada equivalent
[math]\displaystyle{ W_\lambda \equiv EW = \int_{\lambda_1}^{\lambda_2} \frac{F_\text{cont} (\lambda) - F_\lambda}{F_\text{cont} (\lambda)} d\lambda }[/math]
- [math]\displaystyle{ \text{Si } EW \gt 0 \implies \text{ratlla d'absorció} }[/math]
- [math]\displaystyle{ \text{Si } EW \lt 0 \implies \text{ratlla d'emissió} }[/math]
Redshift
[math]\displaystyle{ z = \frac{\lambda_\text{obs} - \lambda_\text{emi}}{\lambda_\text{emi}} \iff 1 + z = 1 + \frac{v_\text{rad}}{c} }[/math] ([math]\displaystyle{ v_\text{rad} }[/math]: velocitat radial, al llarg de la línia de visió)
- Redshift: [math]\displaystyle{ z \gt 0 }[/math]
- Blueshift: [math]\displaystyle{ z \lt 0 }[/math]
Factors que afecten l'observació astronòmica
Factor important de l'atmosfera:
- S'ha de fer fora de l'atmosfera perquè si no s'emporta llum, però no només això agafa llum, també partícules que hi ha per l'espai que tot i que la densitat de l'espai és molt petita com que recorre molta distància sí que s'emporta la llum.
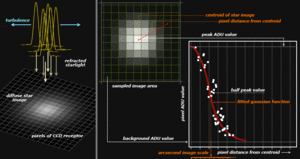
- Efecte de la turbulència (seeing)
- Millors observatoris: fluctuacions de 0.5-1.0 d'arc. seeing-reconstruction-movie.gif
- Per corregir-ho, els telescopis utilitzen òptica adaptativa: envien un làser, i saben com fluctua l'atmosfera, així que saben on apuntar la lent.
Telescopis: no fets de lents (perquè seria molt gran, i en aixecar-ho potser es va cap a baix una mica (potser 3 micres, però ja té efectes rellevants i perdem precisió)), sinó fets de miralls (molts junts de forma hexagonal). Jugant amb els miralls, amb actuadors (molles), es va movent lleugerament el focus que faci que es centri cada cop el fotó que ve de l'objecte que vols observar, per evitar l'efecte seeing.
Enviar un kg a l'atmosfera per la NASA, val 1 milió d'euros.
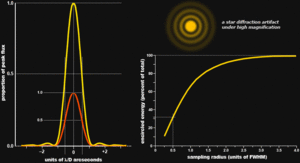
- Disc d'Airi: Quan la llum entra per l'obertura del telescopi, forma un patró d'interferències (es veurà a òptica), i per tant es formaran discs al voltant del punt.
- 1er mínim: [math]\displaystyle{ \sin(\theta) = 1,22 \lambda / D }[/math], on [math]\displaystyle{ D }[/math] és el diàmetre de l'objectiu i [math]\displaystyle{ \theta }[/math] és l'angle de resolució.
Amb la interferometria es pot sintetitzar una D més alta. (però només amb longituds d'ona llargues)
Teorema del límit central -> tindrem una Gaussiana/distribució normal al final.
- Full width half maximum: [math]\displaystyle{ FWHM \approx 2,355 \sigma }[/math] (Gaussiana)
L'atmosfera, per tenir una temperatura, també emet radiació, però per sort no en l'espectre visible (si no no veuríem el cel amb els nostres ulls).
L'amplada del pic principal del disc d'Airi (fora l'atmosfera) és el límit de difracció: [math]\displaystyle{ \frac{D}{\lambda} }[/math]
- Per observar des de la Terra, potser necessitem una certa altura, ja que algunes longituds d'ona no arriben al terra.
@TODO: Include "2007 Thomson Higher Education": gràfica altitude-wavelength (transmission.jpg)
- L'ozó, l'oxígen, el vapor d'aigua, i la pols afecten les ones.
- La Pols:
- Absorció: absorbeix llum i el reemet amb més baixa energia (major longitud d'ona).
- Scattering (dispersió): reemet la llum en una altra direcció de la que procedia.
- "L'ona ha de tenir mida semblant/comparable a la dels obstacles".
- La llum blava és la més afectada per aquest tipus d'interaccions de la pols (així doncs, la pols només s'emporta, selectivament, la llum d'altes freqüències dins de la banda visible (la llum blava)). Això provoca un envermelliment (no és que afegeixi res, sinó que treu el blau).
- Per això el cel es veu blau i les postes de sol es veuen vermelloses.
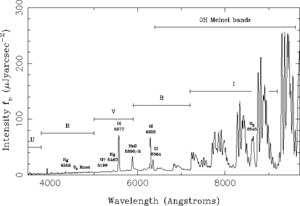
Filtres de banda ampla
@TODO: Incloure foto 'Galaxies in the Universe'
- Filtres:
- V: visible
- B: blue
- R: red
- I: infrared
- Brillantor aparent (flux que ens arriba): [math]\displaystyle{ F_X = \frac{\int_0^\infty T_X F_X(\lambda) d\lambda}{\int_0^\infty T_X(\lambda) d\lambda} }[/math], on X és la banda (B, V, R, ...) i [math]\displaystyle{ T_X \in [0, 1] }[/math] és la transmissió del filtre.
- Magnitud aparent: [math]\displaystyle{ m_x = -2.5 \cdot \log_{10} \left( \frac{F_X}{F_X^0} \right) }[/math], on [math]\displaystyle{ F_X^0 }[/math] és el nivell de referència. Quant més brillant, més petita és el nombre de magnitud aparent (ex: 2), i quant més feble, més gran és el nombre (ex: 40). El 2.5 és perquè això fa que un objecte amb 5 magnituds menys aparents és 100 vegades més brillant.
- Tradicionalment es pren l'estrella Vega com a estrella de referència (i per tant té magnitud aparent 0). Com Vega fluctua, ara el valor es diferent, però no molt diferent perquè les magnituds aparents de les estrelles no variïn molt, i per tant el nivell de referència es pren aproximant-lo al que hi havia per Vega.
Sistema AB (referència absoluta)
[math]\displaystyle{ m_\text{AB} = -2.5 \cdot \log_{10} \left( \frac{\int F_\lambda \cdot T_\lambda d\lambda}{\int T_\lambda d\lambda} \right) - 48.60 }[/math]
- En radioastronomia, com el flux que rebem és menor, necessitem unes altres unitats de potència:
- [math]\displaystyle{ 1 \text{ Jy} = 1 \text{ Jansky} = 10^{-26} \text{W} \cdot \text{Hz}^{-2} \cdot m^{-2} }[/math]